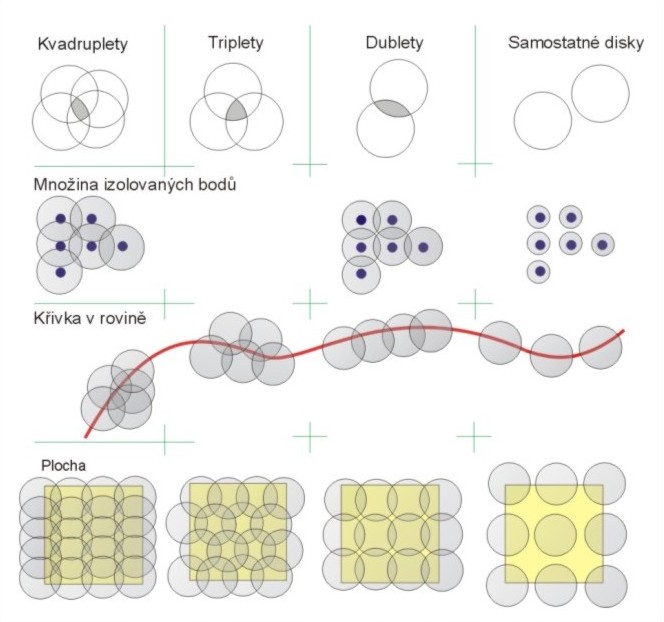
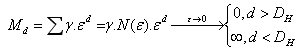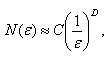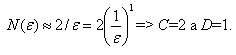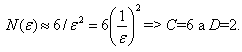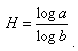Definice fraktálů a fraktální dimenzePřestože pojem fraktální geometrie je znám od konce 70. let 20.stoleti, neexistuje přesná definice fraktálu. V odborné literatuře se lze setkat s různými definicemi fraktálů, které definují pojem fraktál z různých pohledů. Fraktály jsou v podstatě množiny, jejichž geometrický motiv se opakuje ve vlastním mateřském tělese [10, 11] a z tohoto poznatku vychází většina definic. Zde je uvedeno několik nejčastějších a nejvýstižnějších definic, se kterými se lze setkat. Fraktál lze nejjednodušeji definovat jako nekonečně členitý útvar. Opakem nekonečně členitého útvaru je geometricky hladký útvar. Příkladem geometricky hladkých útvarů jsou euklidovská tělesa, jako je přímka, kruh, krychle, koule, atd. Vlastnost fraktálů zvanou soběpodobnost použil Mandelbrot pro jinou definici: Fraktál je tvar tvořený částmi, které jsou podobné celku. Je možné tak definovat soběpodobnostní dimenzi, z které můžeme odvodit fraktální dimenzi. Soběpodobnost a soběafinita však není postačující podmínkou. K tomu abychom mohli mluvit o fraktálu, musí být splněny ještě další podmínky [1, 5, 7]. Fraktální dimenzi lze také definovat pomocí tzv. kapacitní dimenze (capacity dimension): Pokud kapacitní dimenze množiny existuje a není celočíselná, pak se jedná o fraktální dimenzi [2]. ] se lze setkat s podobnou definicí jako od Mandelbrota: Fraktál je objekt, jehož geometrická struktura se opakuje v něm samém. Fraktály se dělí na soběpodobné a soběpříbuzné.Další, snad nejvíce používanou, je definice opět od Mandelbrota: Fraktál je množina, jejíž Hausdorff-Besicovitchova (fraktální) dimenze převyšuje její topologickou dimenzi [1, 5, 7, 8]. Pro tuto definici je nejprve nutné připomenout topologickou dimenzi DT nejlépe pomocí pokrývající dimenze DP. Topologická dimenze DTTopologickou dimenzi používá věda zvaná topologie. Topologie se nezabývá například velikostí geometrických útvarů, ale vlastnostmi, které se deformací otáčením nebo stlačováním nemění. Není důležité zda je objekt kulatý nebo hranatý, velký nebo malý, protože deformací se tyto vlastnosti změní. V topologii je důležité zda je daný objekt spojitý, zda obsahuje otvory, zda je zauzlený a podobně. Topologové se také neomezují na jedno, dvoj či tří dimenzionální euklidovské prostory, ale často pracují v prostorech mnoha dimenzí Topologická dimenze DT je vždy celočíselná. Objekt který je možné homomorfně (zobrazení objektu jednoho na druhém i inverzně) převést stlačováním a ohýbáním na jeden ze simplexů, má stejnou topologickou dimenzi jako simplex. Simplex v tomto případě je bod s topologickou dimenzí 0, úsečka délky 1 s topologickou dimenzí 1, pravoúhlý trojúhelník s odvěsnami délky 1 má topologickou dimenzi 2 a tetraedr má topologickou dimenzi 3. Topologická dimenze je často spojována s charakteristickými objekty pro tuto dimenzi. Objekt s topologickou dimenzi 0 je bod, topologickou dimenzi 1 má přímka, topologickou dimenzi 2 má čtverec a s topologickou dimenzí 3 je to krychle. Pro většinu množin (objektů), s výjimkou patologické množiny, je možné určit jejich topologickou dimenzi pomocí „pokrývající“ dimenze. Jejich hodnoty se rovnají. Pokrývající dimenze DPMnožina bodů, křivka a plocha mohou být pokryty disky několika možnými způsoby jak je znázorněno na obr. 16. Jednotlivé útvary lze pokrývat samostatnými disky, dvojicí disků mající nenulový průnik, tzv. dubletách, třemi kotouči, které mají vzájemný nenulový průnik – triplety a disky, které mají vzájemný průnik čtyř kotoučů – kvadruplety. Pro pokrytí plochy nebo topologicky třídimenzionálního objektu je nutné použít místo disků koule. Při nenulovém průniku dvou koulí se jedná opět o dublety, při nenulovém průniku tří koulí o tripletech, atd. V případě pokrytí křivky v rovině, je křivka pokryta disky čtyřmi různými způsoby (obr. 16 uprostřed). Na úplné pokrytí křivky stačí dublety, tedy pouze jediný průnik dvou sousedních disků a to při jakémkoliv poloměru, pokrývající dimenze je DP = 1.
Množina izolovaných bodů může být pokryta koulemi o nekonečně malém poloměru, takže mezi koulemi nebude žádný průnik. Pokrývající dimenze DP = 0. Plocha má pokrývající dimenzi DP = 2. Na obr. 16 vpravo uprostřed jsou na pokrytí plochy použity dublety a jak je vidět, toto pokrytí není dostačující, neboť plocha není pokryta celá. Na pokrytí je třeba průnik alespoň alespoň tři disků (triplety), jak je znázorněno na obr. 16 dole uprostřed. Podobná myšlenka určuje pokrývající dimenzi například krychle, kdy jsou použity místo disků koule, takže pokrývající dimenze DP =3. Definice pokrývající dimenze je následující: Pokud množina S je pokryta malými disky respektive koulemi, maximální počet disků respektive koulí,
který má vzájemně nenulový průnik, je nazýván uspořádání pokrytí. V případě
dublet je uspořádání rovno dvěma, v případě triplet je to 3 a v případě
kvadruplet je to 4. Otevřená pokrytí množiny S jsou soubory konečně
otevřených disků A={A1,…,Am} takové, že jejich
spojení pokrývá množinu S. Otevřené pokrytí B={Bm,…,Bm}
je nazýváno zjemnění množiny A stanovené pro každé Bi,
v němž je Ak takové že Množina S má pokrývající dimenzi Dp= n právě tehdy, pokud pro libovolný poloměr disku respektive koule r >0 existuje pokrytí množiny S koulemi o poloměru r takové, že každý bod množiny S patří maximálně do n+1 pokrývajících koulí a neexistuje takové pokrytí těmito koulemi, pro které by každý bod z množiny S patřil do n koulí. Dá se dále prokázat, že pro převážnou většinu množin platí DT = DP. Pomocí pokrývající dimenze můžeme tedy definovat dimenzi topologickou. Fraktální (Hausdorff-Besicovitch) dimenze DHDefinice fraktálů pomocí fraktální a topologické dimenze: Útvar je fraktálem pokud platí vztah:
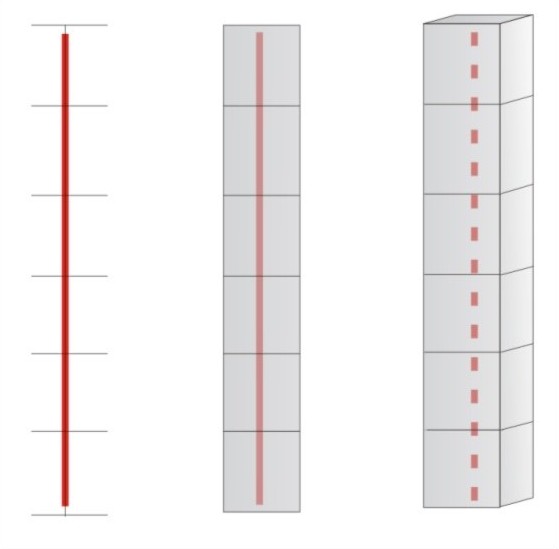
Topologická dimenze DT již byla definována pomocí pokrývající dimenze DP. Fraktální dimenze (Hausdorff-Besicovitch dimenze) DH nemusí být oproti topologické dimenzi celočíselná. Fraktální dimenze také obsahuje informaci o tvaru tělesa. Jinak řečeno, je úměrná míře nepravidelnosti objektu. Vyjadřuje do jaké míry se útvar liší od klasického euklidovského útvaru, který má topologickou dimenzi celočíselnou. Jednoduchým způsobem jak měřit velikost nějakého útvaru S, je pokryt jeho prostor malými boxy o straně e a spočítat počet boxů N(e) potřebných pro pokrytí objektu. Je dán útvar S jako podmnožina prostoru Rn , kde n = 1,2,3 (n=1 pro jednodimenzionální prostoru, n=2 pro dvojdimenzionální prostor a n=3 pro třídimenzionální prostor). n-dimenzionálním boxem v Rn je uzavřený interval pokud n=1, čtverec pokud n=2 a krychle pokud n=3. Je předpokládaná úsečka (obr. 17) o délce L0, kde počet N boxů délky e je N(e)=L0 /e.
Délka úsečky je pak dána vztahem:
kde N(e) je počet boxů o délce e nutných na pokrytí úsečky. Pokud se délka boxu budeme zmenšovat až k lim e->0, pak se spočítaná délka L(e) bude asymptoticky blížit k délce skutečné L0. Tedy :
Je zřejmé, že délka L0 je nezávislá na e, tedy je nezávislá na měřítku. Je nutné zdůraznit, že v tomto případě se stále jedná o euklidovský geometrický útvar - úsečku. Pokud bude měřena plocha A úsečky, pak počet boxů je opět N(e) a boxy mají plochu e2 (obr. 7 uprostřed). Plocha je dána vztahem:
Plocha úsečky je samozřejmě rovna nule. Podobně lze spočítat objem:
Plocha a objem přímky konvergují k nule jak se e zmenšuje. Užitečnou mírou pro popis přímky je pouze délka. Pokud bude podobným způsobem změřena plocha (obr. 18), měří se u ní povrch A:
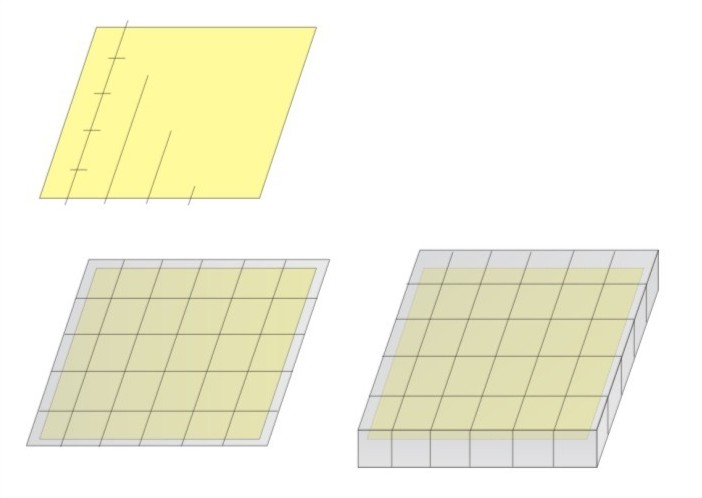
Počet boxů potřebných pro pokrytí plochy je N(e)=A0 /e2. Když se e blíží nule, povrch plochy je A0. Objem plochy je:
Formálně lze vypočítat délku plochy:
Délka plochy je samozřejmě nekonečná. Užitečnou mírou je pouze povrch plochy. Pomocí zobecnění těchto měření rozměrů lze definovat fraktální (Hausdorff-Besicovitchovou) dimenzi. Měření množiny
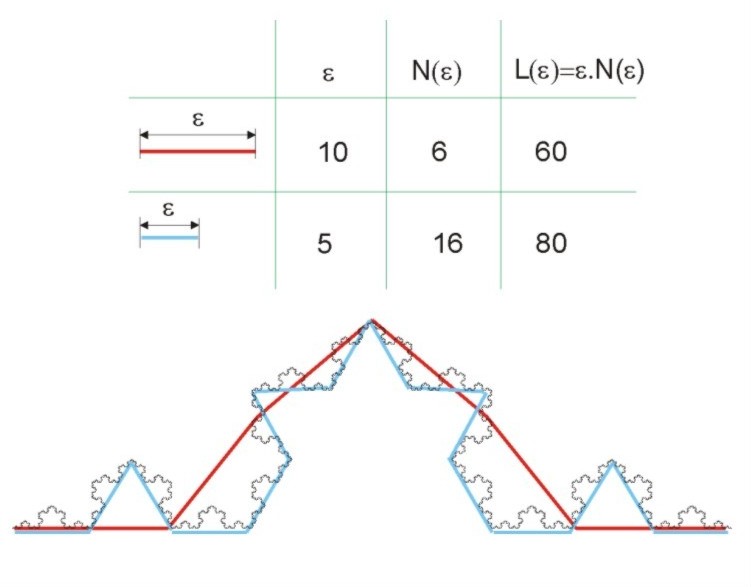
kde N(e) je opět počet boxů potřebných pro pokrytí množiny S. Pro případ dříve uvedené plochy je objem V=0 a d=3, délka L=¥ a d=1. ). V tomto případě je tedy fraktální (Hausdorff-Besicovitchova) dimenze DH =2. Topologická dimenze plochy DT=2, tedy fraktální dimenze, se rovná topologické DT=DH. Hladká plocha tedy není fraktál. Podobně ani přímka, krychle či jakékoliv jiné euklidovské těleso není z geometrického hlediska fraktálem. Jiné je to například s Kochovou křivkou. Jednou ze zásadních vlastností fraktálu je závislost celkové délky L(e) na zvoleném měřítku. Při zmenšování délky boxu e, kterým budeme měřit délku Kochovy křivky, se celková délka neblíží ke konečné hodnotě, ale roste. Jako příklad jsou na obr. 19 uvedeny dvě zvolené míry: e =10 a e = 5. N(e) je počet úseček o délce e; nutných na změření a L(e) je spočítaná délka (L(e)=N(e).e). Jak je zřetelně vidět, při použití menší míry se délka prodlouží.
Pokud se bude délka úsečky (boxu) dále zmenšovat až k lim e->0, pak pro Kochovu křivku získáme délku nekonečnou:
Vhodné porovnat s (5). Pokud by byl měřen povrch Kochovy křivky, vyjde:
Kochova křivka tedy musí mít fraktální dimenzi mezi hodnotou 1 a 2. Pomocí vztahu (11) a dalších jeho úprav by se dalo dokázat, že Kochova křivka má fraktální (Hausdorff-Besicovitchovou) dimenzi DH=1,2619 ( Fraktální (Hausdorff-Besicovitch) dimenze DH ). Kochova křivka je tedy fraktál. Představuje něco mezi hladkou křivkou a hladkou plochu, ale více se blíži hladké křivce. Je nutné zdůraznit, že tyto vztahy platí pro útvary s fraktální dimenzí 1<DH<2. Se závislostí celkové délky na zvoleném měřítku se setkáváme i u dalších přírodních útvarů, jako jsou například délky hranic, břehy řek, pobřežní linie atd. Vůbec poprvé se tímto problémem podrobně zabýval Richardson. Ten měřil obvod (pobřežní linii) ostrova Korsika. Čím byla větší přesnost jeho měření, tím byla naměřená délka vyšší. Také jako první zjistil, že obvod ostrova je závislý na délce tyče, kterou se měří a empiricky odvodil vztah:
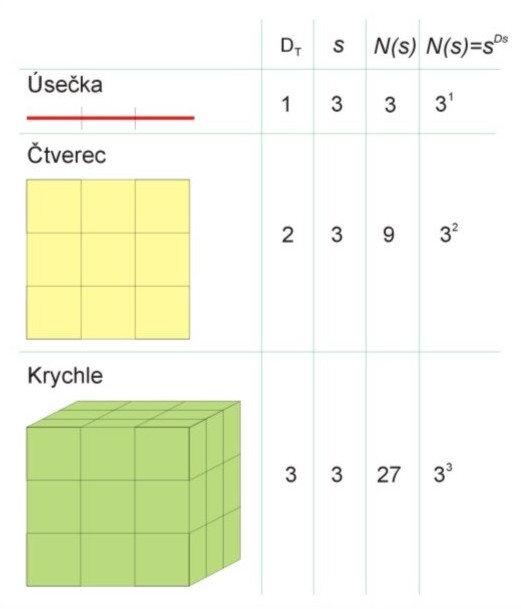
kde LK je naměřenou délkou, N(e) je počet boxů (v tomto případě úseček) o délce e potřebných k pokrytí (aproximaci) dané křivky (porovnej se vztahem (5) a (12)). Důvodem je již zmíněná měřítková závislost, kdy při měření značně složitého útvaru pomocí velkého měřítka je spousta drobných detailů nezměřena, nebo také zanedbána, ale tyto drobné detaily jsou pak zohledněny při zvětšování měřítka a v důsledku toho délka narůstá. Tento jev označujeme jako Richardsonův efekt. To co se ukázalo být zajímavé je, že délka pobřeží je závislá na konstantě D. Význam této konstanty si Richardson nedokázal vysvětlit, teprve Benoit Mandelbrot dokázal souvislost této konstanty a Hausdorff-Besicovitch (fraktální) dimenzí. Definice fraktálu pomocí soběpodobnostní dimenze DSFraktál je tvar tvořený částmi, které jsou podobné celku. Tato definice využívá tedy pojem soběpodobnosti (anglicky self-similarity). Nicméně soběpodobnost není postačující podmínkou pro to, aby bylo možno daný objekt označit jako fraktál. Úsečka, čtverec a krychle uvedené na obr. 20, jsou rozděleny na malé kopie celku pomocí faktoru změny měřítka s=3.
Vztah mezi počtem částí N na které se těleso rozdělí (faktor změny délky) a faktorem změny měřítka s je dán:
Vztah lze pak upravit dále na :
DS je soběpodobnostní dimenze. DS =1 pro přímku, DS=2 pro plochu a DS =3 pro krychli. Tyto dimenze jsou shodné jak s fraktální(Hausdorff-Besicovitchovou) dimenzí DH, tak i s topologickou dimenzí DT. Proto se nejedná o fraktály stejné, jak bylo dokázáno v předchozí kapitole. V případě Kochovy křivky, byly všechny úsečky rozděleny na tři části. Faktor změny měřítka s je tedy 3. V každém kroku byly vloženy dvě úsečky na místo jedné o délce 1/3 celkové délky. Počet částí N (faktor změny délky) na které se těleso rozdělilo v každém kroku je pak 4. Tedy
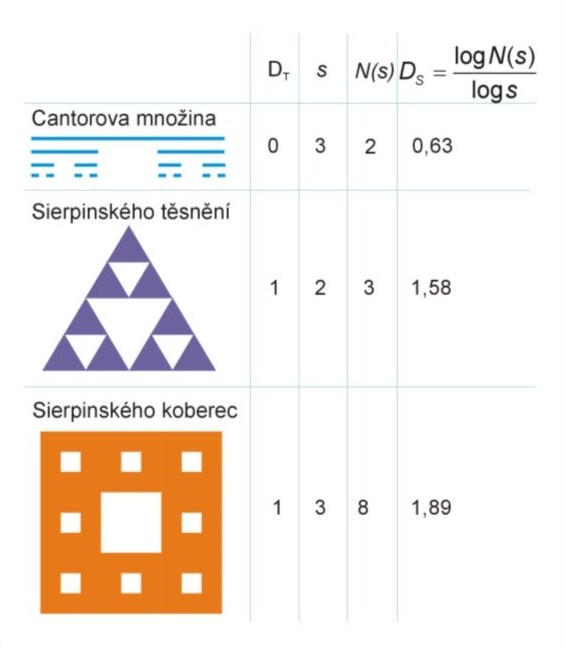
Kochova křivka má soběpodobnostní dimenzi DS=1,269 a ta je rovna fraktální (Hausdorff-Besicovitchovy) dimenzi DH. Výsledek není celočíselný, fraktální dimenze je vyšší než topologická (DT Koch=1). Kochova křivka je fraktál. Na obr. 21 je uvedeno několik příkladů matematických deterministických fraktálů. Je zde uvedena topologická dimenze DT a soběpodobnostní dimenze DS. Cantorova množina (angl. Cantor set) je generovaná odstraněním prostřední třetiny úsečky. V následujících krocích je opět u všech úseček odstraněna prostřední třetina. Při opakování v tomto algoritmu do nekonečna je získána Cantorova množina .
V tomto případe je faktor změny měřítka s=3 (stejně jako u Kochovy křivky). Protože nebyla žádná usečka vkládaná, je počet částí N (faktor změny délky), na které se těleso v každém kroku rozdělí N=2. Po dosazení do vztahu (16) obdržíme fraktální dimenzi pro Cantorovu množinu DH=0,6309. Tento útvar je více než izolovaný bod, ale méně než hladká křivka. Jak již bylo uvedeno v kap. Jak lze fraktály rozčlenit, jaká je jejich konstrukce Sierpinského těsnění lze například generovat rozdělením plochy trojúhelníku na čtyři menší a odstraněním prostředního trojúhelníku z původního (obr. 7) Faktor změny měřítka je s=2. Tedy každá hrana objektu je rozdělena na dvě části. Po vyjmutí prostřední části, je získáno v každém kroku třikrát více samostatných částí, faktor změny délky je tedy N=3. Pokud bude procedura generování opakována do nekonečna, je získán objekt s fraktální dimenzí DH=1,58496, kterou lze spočítat pomocí vztahu (16). Sierpinského těsnění je více než hladká křivka, ale méně než hladká plocha. Sierpinského koberec je generován podobně jako těsnění, ale iniciátorem je
čtverec. Tuto proceduru si lze představit jako rozdělení čtverce na devět malých
čtverců a vyjmutím prostředního. Objekt má pak fraktální dimenzi DH=1,8928.
Definice fraktálu pomocí kapacitní dimenze DKPokud kapacitní dimenze útvaru (množiny) existuje a není celočíselná, pak se jedná o Hausdorff-Besicovitch (fraktální) dimenzi [2]. Mějme množinu S jako úsečku v intervalu [0,2], obr. 22.
 , kde N(e) je
počet boxů při velikosti boxu e.
Samozřejmě, pokud 2/e není
celočíselné, pak  . Například, pokud e =3/7
(jako v tomto případě), pak počet boxů nutných k pokrytí intervalu [0,2] je N(3/7)=5,
kdežto, když dosadíme za e , pak  . Ovšem je
možné zapsat  . S
tím jak se však eblíží k 0,
N(e) je úměrné k 1/e.
Pokud je množina S obdélníkem
[0,2] x [0,3] (obr. 22), pak pro malé e >0
je získáno přibližně
V případě podmnožinu S množiny
(prostoru) Rn, kde n=1,2,3., jsou uvažovány hodnoty C >0
a
kde e se blíží k 0. Pro úsečku v intervalu [0,2] tedy platí:
Pro obdélník [0,2] x [0,3]:
Rovnici (18) lze dále upravit, tak aby byl získán vztah pro D. Nejprve je rovnice zlogaritmována:
Z tohoto vztahu se pak získá:
Druhou část rovnice lze zanedbat, protože se bude blížit k 0 s tím, jak se k 0 bude blížit e. Vztah má pak tvar:
Pokud existuje limita vztahu (23), když se e blíží k 0, definuje se D jako kapacitní dimenze množiny S. Definice: Mějme množinu S jako podmnožinu Rn, kde n=1,2 nebo 3. Kapacitní dimenze (box dimenze) množiny S je dána vztahem:
pokud existuje limita. Pokud kapacitní dimenze existuje a není celočíselná, pak množina S má fraktální (Hausdorff-Besicovitchovu) dimenzi. Kapacitní dimenzi lze také použít pro výpočet fraktální dimenze matematických deterministických fraktálů. Vztah (24) však musí být upraven a musí být dokázána jeho platnost:
kde k je počet kroků iterace (opakování), N(rk) je počet částí na které se těleso rozdělí (z předchozí kapitoly známý faktor změny délky) a r je změna měřítka nově rozdělených částí pro kterou platí 0<r<1. Dá se dokázat, že vztah (25) existuje jen pokud existuje vztah (24). [2]. Příkladem může být opět Cantorova množina, která je generována vyjmutím prostřední třetiny z intervalu [0,1]. Po každém kroku je získáno dvakrát více segmentů než v předchozím kroku a každý segment je třetinový. Tedy N(1/3)=2 a z toho po dosazení N(1/3k)=2k pro každé k³1. Změna měřítka rozdělených částí je r=1/3. Ze vztahu (25):
Kapacitní dimenze není celočíselná, tedy se jedná o fraktální dimenzi DH=0,6309. Tato hodnota se shoduje s hodnotou vypočtenou pomocí soběpodobnostní dimenze v Definice fraktálu pomocí soběpodobnostní dimenze DS . Bylo by možné ji vypočítat i podle vztahů uvedených v Fraktální (Hausdorff-Besicovitch) dimenze DH . Podobným způsobem jako byla vypočtena kapacitní dimenze Cantorovy množiny, lze vypočítat dimenzi Sierpinského těsnění. Tato množina je generována z plochy rovnostranného trojúhelníka o délce stran 1. V každém kroku je získáno třikrát více trojúhelníků než v předcházejícím kroku. Délka stran je po každém kroku poloviční, tedy N(1/2k)=3k a r=1/2. Za použití vztahu (25):
Opět není vypočtená kapacitní
dimenze celočíselná. Fraktální dimenze je DH=1,585.
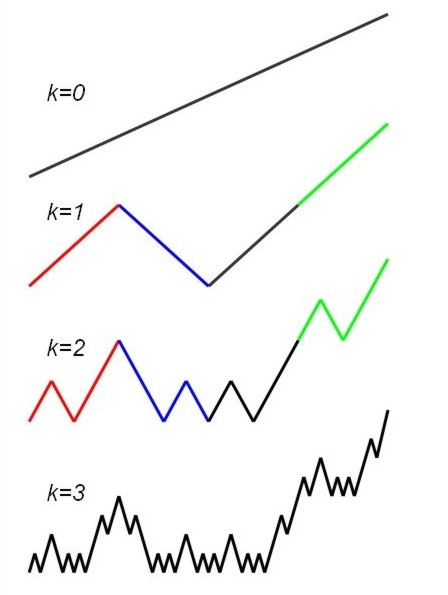
Soběpříbuznost a Hurstův exponentSoběpodobné fraktály mají specifické vlastnosti. Pokud je například vyjmuta malá část z celého fraktálu a je zvětšena stejně ve všech směrech (izotropicky), bude originál i zvětšenina vypadat stejně [1,5, 7]. Vedle soběpodobných fraktálů se lze v matematice i v přírodě často setkat s tzv. soběpříbuznými (soběafinitními) fraktály. Pokud se má po zvětšení dosáhnout stejného výsledku jako u soběpodobných fraktálů, je nutné zvětšovat vyjmutou část v různých směrech jinak (anizotropicky). Jednoduchý model generování soběpříbuzného fraktálu je na obr. 2.23. Tato struktura je neměnná při
anizotropickém zvětšení
Všeobecně, pokud je křivka měřítkově neměnná (má po zvětšení stejný charakter)
při transformaci
H je tzv. Hurstův koeficient. Po úpravě výrazu (29) obdržíme:
V případě křivky generované na obr. 23 platí H = 1/2. Řešení rovnice (29)
je jednoduše Soběpříbuzné fraktály jsou často signály - časové řady. Jsou to objekty které mají z topologického hlediska dimenzi DT=1. Vztah mezi Hurstovým koeficientem a fraktální (Hausdorff-Besicovitch) dimenzí je dán vztahem:
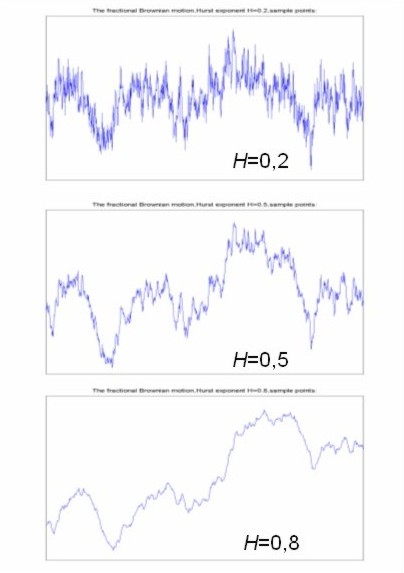
Hurstův koeficient je od 0 do 1 a stejně jako fraktální dimenze, uvádí charakter objektu. V případě časové řady, složitější řada z pohledu struktury je popsán nižším Hurstovým koeficientem, tedy vyšší fraktální dimenzí. Jednodušší (často hladší) časová řada má vyšší Hurstův koeficient a nižší fraktální dimenzi. H = 0 prezentuje tzv. růžový šum; H = 0,5 Brownianův šum; H = 1 je černý šum. Po určité transformaci může být Hurstův koeficient použit také pro další části spektra šumu. Příklady časových řad a jejich Hurstova koeficientu jsou uvedeny na obr. 24 pro simulaci Brownianova pohybu užitím Cholesky-Factorizace odpovídající kovarianční matice.
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
(množina Bi je podmnožinou množiny Ak).
Uspořádání pokrytí množiny A
maximální celočíselné k takové, že existují disjunktivní (nespojité) indexy i1,…,ik
s 
.
je dáno testovací funkcí
určenou pro pokrytí množiny S.
boxů pro její pokrytí.
, takové, že:
,
.
Při samotné konstrukci bylo totiž použito pravidlo: v ose x se při každé
iteraci rozdělí úsečka na 4 díly, kdežto v ose y pouze na 2 díly. Pokud je
vyjmuta malou část z originálu fraktálu (s n->
,
pak platí:
.
K získání stejného charakteru po zvětšení, je třeba
transformační koeficient, tzv. Hurstův exponent. Ten uvádí, jak musí být
fraktál transformován z pohledu měřítka, aby bylo dosáhli stejného charakteru po
zvětšení.
