Fraktální geometrie a fraktály

Do doby, než byla objevena a popsána fraktální geometrie, byla euklidovská geometrie považována za nejsilnější nástroj popisu všech geometrických útvarů. Euklidovská geometrie byla s úspěchem používána po celá staletí, avšak její slabinou, kterou si prakticky nikdo neuvědomoval, byl problém jak popsat jednoduchým způsobem složitě strukturované útvary. Tyto útvary mohly být jak matematického, tak i přírodního původu.

Běžné objekty jako úsečky, kruhy, čtverce, trojúhelníky, obdélníky, koule, krychle, jehlany lze poměrně snadno popsat pomocí euklidovské geometrie. Například pravoúhlý trojúhelník je plně popsán (každý jeho bod je jednoznačně určen) Pythagorovou větou [10, 11]. Pokud by bylo třeba popsat jednoduchý fraktál jako je například Kochova křivka (obr. 2.1), pak by bylo nutné stanovit složitou a nepřehlednou rovnici. Tento objekt však může být jednoduše popsán pomocí fraktální geometrie. Její složitost lze dokonce popsat pomocí jednoho čísla, tzv. fraktální dimenze.

K pochopení celého problému je vhodné si odpovědět na pět základních otázek:

• Co je to fraktální geometrie a fraktál?
• Co je to fraktální (Hausdorff-Besicovitchova) dimenze?
• Jak lze fraktály rozčlenit, jaká je jejich "konstrukce"?
• Jaké mají fraktály vlastnosti?
• Kde se fraktály vyskytují?

Fraktální geometrie je matematický nástroj pro popis složitě strukturovaných objektů, jejichž charakter se nemění při určitém zvětšení nebo zmenšení. Vhodným příkladem je tvar pobřežní linie. Pokud jsou srovnány dvě mapy různých měřítek, pak charakter pobřežní linie se nemění – pobřeží na obou mapách vypadá stejně. To znamená, že pobřežní linie je měřítkově neměnná, či jinak, nemá charakteristické délkové měřítko [1]. Benoit Mandelbrot si položil jinou otázku: Jaká je podstata tvaru pobřeží? Ta se stala mezníkem úvah v jeho práci: „Jak dlouhé je pobřeží Velké Británie?“ (1977). Tato na první pohled jednoduchá otázka však po chvíli úvah nabývá hlubšího smyslu. Mandelbrot vyšel z poznatků Richardsona, který měřil ostrov Korsiku( více v kapitole Fraktální (Hausdorff-Besicovitch) dimenze DH a Obvodová metoda . Mandelbrot použil pro změření délky pobřeží Velké Británie nejprve satelitních map, v druhém případě pak map turistických. Došel k závěru, že délka změřená z map turistických je 2x až 3x delší než délka změřená z  map satelitních. Důvod je následující: turistické mapy jsou mnohem podrobnější než mapy satelitní, což způsobí, že při měření délky pobřeží pomocí mapy satelitní je mnoho detailů zanedbáno či přehlédnuto a tyto detaily se projeví jako důležité při měření z map turistických. Richardson empiricky odvodil vztah mezi délkou a měřítkem. Mandelbrot pak našel souvislosti v tomto vztahu s Hausdorffovou dimenzí a mohl tak označit pobřežní linii za fraktál [5, 7, 11].

Označení fraktál tedy poprvé použil B. Mandelbrot. Ten je také označován za „otce“ fraktální geometrie. Je však pravdou, že matematické objekty dnes označované jako klasické fraktály (přesněji matematické deterministické fraktály), byly objeveny mnohem dříve, včetně Kochovy křivky. Mandelbrot však tyto objekty popsal, nazval a spolu s dalšími matematiky sjednotil teorii, která je označována jako fraktální geometrie. Mandelbrot slovo „fraktál“ použil pro všeobecné označení objektů, jejichž tvar je nezávislý na velikosti měřítka, pod kterým objekt pozorujeme (měřítková neměnnost). Vyšel z významu latinského slova "fractus". Z něj odvozené slovo "frangere" znamená "rozlámat" - vytvořit nepravidelné úlomky. Jako fraktály se tedy označují nepravidelné geometrické útvary dělitelné na jednotlivé části, z nichž každá je v ideálním případě zmenšenou kopií celku. Jsou to tedy množiny, jejichž geometrický motiv se opakuje v základním tělese a tento jev je nazýván soběpodobnost (self-similarity). Objekt je tedy striktně soběpodobný (deterministický), pokud může být rozdělen na libovolně malé části, které jsou malou replikou původní množiny [1, 2, 3, 4, 6, 7, 8, 9, 10, 11]. Matematické fraktály mohou být také statisticky soběpodobné (stochastické), stejně jako fraktály přírodní, kdy jsou malé úlomky podobné celku jen statisticky..

Vedle soběpodobných fraktálů existují také fraktály soběafinitní (self-affined, soběpříbuzné). U těchto fraktálů je třeba znát vedle struktury nepravidelných úlomků i způsob transformace měřítka (více v Soběpříbuznost a Hurstův exponent . Čtenář se může také setkat s názvem samopodobnost. Dál se lze setkat s pojem soběpříbuznost [11],který charakterizuje objekty, jejichž kterýkoliv výsek je podobnou kopií původního tělesa.

Ve fraktální geometrii je počítána nebo odhadována tzv.fraktální dimenze, která je „charakteristickým číslem“, udávajícím jak složitý je pozorovaný útvar. Může se jednat o povrch nebo strukturu tělesa, časovou řadu nebo množinu bodů. Fraktální dimenze (lze se také setkat s pojmem Hausdorff-Besicovitchova dimenze) matematicky popisuje složitost těchto objektů (více v Fraktální (Hausdorff-Besicovitch) dimenze DH).Fraktální dimenze, v případě fraktálů, převyšuje jejich topologickou dimenzi, která je celočíselná (dimenze charakterizované bodem, úsečkou, trojúhelníkem a tetraedrem). Z tohoto předpokladu vychází také jedna z definic fraktálů.

Fraktály lze dále dělit podle různých pravidel a podle různých autorů. Tento web využívá prvně uvedeného rozdělení IFS a TEA a podrobnější rozdělení je v kapitole Rozdělení fraktálů. Vysvětlení konstrukce IFS fraktálů je možné podat například pomocí již zmíněné Kochovy křivky. V případě této křivky potřebujeme mít tzv.

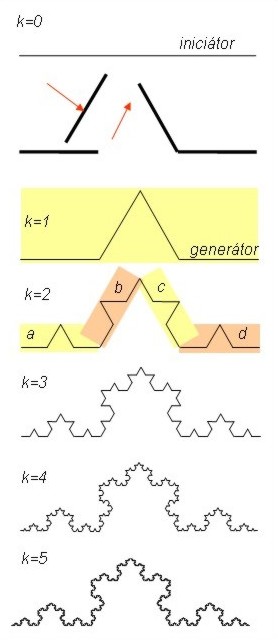Obr. 2 Generování Kochovy křivky

iniciátor a generátor. Iniciátor v tomto případě představuje úsečku (krok 0, obr. 2) a generátor je tvar, kterým se iniciátor nahradí. V tomto případě je generátorem útvar vzniklý vyjmutím prostřední třetiny a nahrazením této třetiny dvěma úsečkami délky jedné třetiny. Tuto transformaci si lze také představit jako přerušení úsečky v jedné třetině a nadzvednutí druhé třetiny tak aby bylo možné vložit novou úsečku délky opět jedné třetiny. Po transformaci je každá strana už považována za iniciátor pro další krok. V každém kroku se nahrazuje každá úsečka (iniciátor) zmenšenou kopií generátoru. Jak je vidět na obr. 2, již v kroku 5 lze získat poměrně komplikovanou křivku.

Generaci tohoto typu fraktálů je lépe si představit z matematického hlediska jako konstrukci pomocí takzvaných afinních transformací. Těmito transformacemi se rozumí: zmenšení, rotace a posuv. V případě Kochovy křivky je pro generaci použito všech tří transformací. Postup těchto transformací je znázorněn na obr. 2 světle šedou a tmavě šedou výplní. Generátor v kroku 1 je ve druhém kroku uplatněn čtyřikrát. Pro levou část kroku (a) je generátor pouze zmenšen na 1/3. Pro druhou návaznou část (b – tmavě šedá výplň) je generátor zmenšen na 1/3, posunut na 1/3 a pravý konec otočen o 60o proti směru hodinových ručiček. Třetí část (c) je také zmenšena na 1/3, posunuta o 1/3, ale levý konec je otočen o 60o ve směru hodinových ručiček. Poslední část je opět zmenšena na 1/3 a posunuta na 2/3. [10, 11].

Přírodní fraktály oproti matematickým nejsou nikdy striktně soběpodobné, tedy přírodní útvary při zvětšení nejsou přesně identické. Příkladem přírodního fraktálu je již zmíněná pobřežní linie v Obvodová metoda To je objekt s fraktální dimenzí mezi 1 a 2. S objekty, které lze od určitých měřítek z geometrického hlediska nazvat  fraktály, se lze setkat v přírodě i jinde. V této souvislosti lze mluvit o struktuře na struktuře. Například kamenné pohoří má při pohledu z dálky svoji strukturu, kterou tvoří hory, kopce a vyvýšeniny. V případě přiblížení lze vidět jednu horu, která je opět strukturovaná. Po dalším přiblížení lze vnímat mimo jiné kamení, které má opět strukturu. Po odlomení části této struktura a po dalším zvětšení se objeví další struktura. Při dalším zvětšování bude pozorována další a další struktura, což bude pokračovat až po atomární délky. Jedná se tedy o strukturu na struktuře jak je znázorněno na obr. 3.

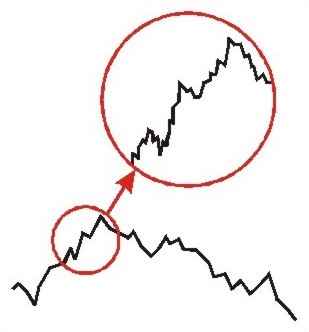Obr. 3 Struktura na struktuře

Dalším příkladem může být sněhová vločka a její nádherně složitá struktura. Popis pomocí euklidovské geometrie by byl prakticky nemožný. Pokud by se povedlo přece jen sněhovou vločku popsat, pak výsledky budou omezeny pouze na tento jediný exemplář. Každá další vločka bude jiná, jedinečná a bude se třeba jen mírně lišit od těch ostatních. Nikdy před tím a ani nikdy v budoucnu nedopadne na zem stejná vločka. To je způsobeno neopakovatelnými podmínkami, při kterých vločka vzniká. Stejně tak jako vločka, je každé těleso útvar, množina či povrch v reálném světě unikátem, který nelze absolutně přesně reprodukovat. Lze vytvořit podobný objekt, ale nikdy ne kopii.

Fraktály jsou pohoří, oblaka, blesky, sněhové vločky, toky řek, stromy i listí, cévní systémy živočichů, komůrky v plicích, DNA, dále i rozložení hmoty v galaxiích, hvězdokupy, ale i povrch obrobku, tvar trhlin i vad v obrobku i nástroji, či dokonce časový vývoj akcií na burzách všeho druhu, časové změny inflace, zadlužení států i vývoj kurzu měny. Dá se říci, že fraktály jsou všude v okolí. Euklidovská tělesa, jako například přímky, čtverce či krychle, jsou pouze v učebnicích matematiky. Laik se tedy musí vzdát klasických představ o tělesech kolem, ale i dějích kolem nás a spíše než poznat, uvěřit, že náš svět je strukturovaný.

Neznamená to však, že by nebyla euklidovská geometrie v běžném světě použitelná. Například obyčejný stůl, skládá se ze čtyř nohou a desky. Nohy budou pro zjednodušení jen válce stejného průměru, deska bude mít konstantní délku, šířku a tloušťku. Tento objekt v běžném měřítku bude popsatelný pomocí euklidovské geometrie. Pokud by byl posuzován jeho povrch, který by byl náležitě zvětšen, pak se lze setkat se strukturou na struktuře. Povrch je pak z geometrického hlediska označen jako fraktál. Jiným příkladem je strom, který je z geometrického hlediska i v běžném měřítku je fraktálem.

Protože fraktály se z geometrického hlediska v přírodě vyskytují a jsou její přirozenou součástí, je znalostí fraktálů využíváno i při simulacích reálného světa ve virtuální realitě, počítačových hrách a ve filmu. Příkladem může být povrch měsíce ve filmu Apollo 13 režiséra Rona Howarda nebo Titanik, Den po té a další. K  tomu, aby bylo možno generovat tyto přírodní struktury, musí být známa mimo jiné fraktální dimenze. U přírodních fraktálů není ovšem znám „algoritmus generování“ útvaru a fraktální dimenzi lze jen odhadovat (Odhad fraktální dimenze).

Přírodní fraktály jsou často multifraktály. Tento pojem značí, že fraktál v  určitých měřítkách má jinou složitost (jiné vlastnosti). To je dáno různou váhou vlivů působících na vznik fraktálu v různých měřítkách. Multifraktály mohou být také generovány „uměle“, tzv. matematické multi-fraktály.